Integrales de funciones racionales
![f(x) = \frac{P(x)}{Q(x)}, \qquad P(x),Q(x)\in \R[x]](http://upload.wikimedia.org/wikipedia/es/math/8/e/4/8e418aac8dbe42c60615386abe8a0d10.png)
Si el denominador es un polinómico mónico 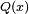 con k raíces diferentes, entonces admitirá la siguiente factorización en términos depolinomio irreducibles:
con k raíces diferentes, entonces admitirá la siguiente factorización en términos depolinomio irreducibles:
Si 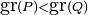 entonces la función racional puede escribirse como combinación lineal de fracciones racionales de las formas:
entonces la función racional puede escribirse como combinación lineal de fracciones racionales de las formas: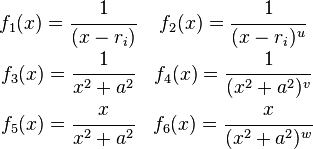
Por lo que la integral de la función  es una combinación lineal de funciones de la forma:
es una combinación lineal de funciones de la forma:
Obsérvese que lo anterior implica que las funciones racionales constituyen un cuerpo algebraico que es cerrado bajo la derivación, pero no bajo la integración.
![f(x) = \frac{P(x)}{Q(x)}, \qquad P(x),Q(x)\in \R[x]](http://upload.wikimedia.org/wikipedia/es/math/8/e/4/8e418aac8dbe42c60615386abe8a0d10.png)
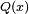 con k raíces diferentes, entonces admitirá la siguiente factorización en términos depolinomio irreducibles:
con k raíces diferentes, entonces admitirá la siguiente factorización en términos depolinomio irreducibles:
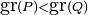 entonces la función racional puede escribirse como combinación lineal de fracciones racionales de las formas:
entonces la función racional puede escribirse como combinación lineal de fracciones racionales de las formas: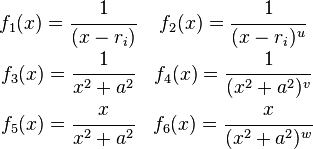
 es una combinación lineal de funciones de la forma:
es una combinación lineal de funciones de la forma:
Integración por partes
Este método permite resolver un gran número de integrales no inmediatas.
1. Sean u y v dos funciones dependientes de la variable x; es decir, u = f(x), v = g(x).
2. La fórmula de la derivada de un producto de dos funciones, aplicada a f(x).g(x), permite
escribir, d(f(x).g(x)) = g(x).f´(x)dx + f(x).g´(x)dx
escribir, d(f(x).g(x)) = g(x).f´(x)dx + f(x).g´(x)dx
3. Integrando los dos miembros,
∫ d[f(x).g(x)] =∫ g(x).f´(x).dx + ∫ f(x).g´(x).dx
De la misma manera que ∫ dx = x, también ∫ d[f(x).g(x)] = f(x).g(x)
Por tanto, f(x).g(x) = ∫ g(x).f´(x).dx + ∫ f(x).g´(x).dx.
De aquí se obtiene que:
∫ f(x).g´(x).dx = f(x).g(x) - ∫ g(x).f´(x).dx
Esta no es la fórmula usual de la integración por partes.
Puesto que u =f(x), du = f´(x)dx, y al ser v = g(x), dv = g´(x)dx. Llevando estos resultados a la igualdad anterior,
∫ u.dv = u.v - ∫ v.du
Ejercicio: integración por partes
1) Calcular ∫ ln x dx
Resolución:
Este es uno de los casos más sencillos; la integral consta de una sola función, ln x.
Haciendo u = ln x, y diferenciando, du = dx/x
Necesariamente, dv = dx. Integrando ambos miembros, ∫ dv =∫ dx. Es decir, v = x.
Aplicando la fórmula, ∫ ln x dx = x.ln x - ∫ x.(1/x).dx = x.ln x - x + C
integracion por sustitucion o cambio de variable
El método de integración por sustitución o cambio de variable se basa en la derivada de la función compuesta.
Para cambiar de variable identificamos una parte de lo que se va a integrar con una nueva variable t, de modo que se obtenga una integral más sencilla.
Pasos para integrar por cambio de variable
1º Se hace el cambio de variable y se diferencia en los dos términos:
Se despeja u y dx, sutituyendo en la integral:
2º Si la integral resultante es más sencilla, integramos:
3º Se vuelve a la variable inical:
Ejemplo
Cambios de variables usuales
1. 
2. 
3. 
4. 

5. En las funciones racionales de radicales con distintos índices, de un mismo radicando lineal ax + b, el cambio de variable es t elevado al mínimo común múltiplo de los índices.
6. Si  es par:
es par:










No hay comentarios:
Publicar un comentario