OBJETIVOS GENERALES
· Posibilitar que el estudiante use eficientemente las herramientas tecnológicas a su alcance, en la solución de los problema.
· Estudiar los conceptos de integral y antiderivada de funciones reales de variable real.
OBJETIVOS ESPECÍFICOS
· Desarrollar en el estudiante la habilidad para aplicar el Teorema Fundamental del Cálculo, en el cálculo de integrales definidas.
· Desarrollar en los alumnos habilidades tanto para la comprensión de la demostración de teoremas como para la obtención de conclusiones sólidas a partir de hipótesis dadas y su capacidad para idear demostraciones.
· Propiciar que el estudiante aprenda a trabajar adecuadamente en grupo y también de manera individual.
 ó
ó 
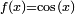 en
en  es la función
es la función  ya que:
ya que: